Sommaire
Cliquez sur le titre d'une partie pour accéder directement à son contenu.
1. La fraction-partage
a) Vocabulaire
Une fraction est une écriture de la forme $\frac{a}{b}$ où $a$ et $b$ sont des nombres entiers, avec $b$ différent de $0$. Le nombre $a$ est appelé le numérateur et le nombre $b$ est appelé le dénominateur.
$\frac{5}{8}$ est une fraction. Son numérateur est $5$ et son dénominateur est $8$.
b) Représentation d'un partage
Une fraction permet de représenter un partage.
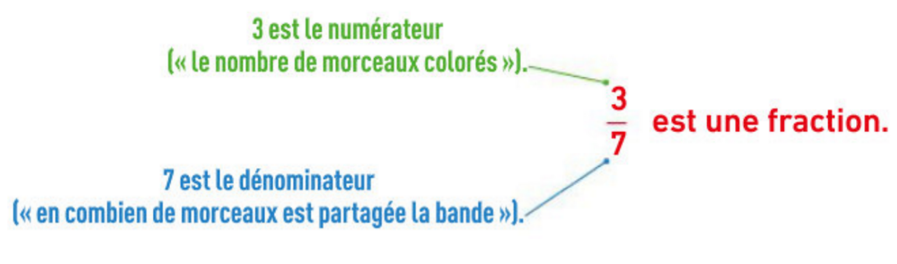
Dans chaque cas on indique quelle fraction de la figure est coloriée.
a) Il y a $8$ parts au total et $4$ parts sont coloriées. La fraction associée est donc $\frac{4}{8}$.
b) Il y a $6$ parts au total et $2$ parts sont coloriées. La fraction associée est donc $\frac{2}{6}$.
c) Il y a $10$ parts au total et $3$ parts sont coloriées. La fraction associée est donc $\frac{3}{10}$.
d) Il y a $9$ parts au total et $3$ parts sont coloriées. La fraction associée est donc $\frac{3}{9}$.
c) Fractions et demi-droite graduée
Une fraction permet de repérer un point sur une demi-droite graduée.
Sur la demi-droite ci-dessous, on a placé différents points et leur abscisse est exprimée à l'aide d'une fraction.
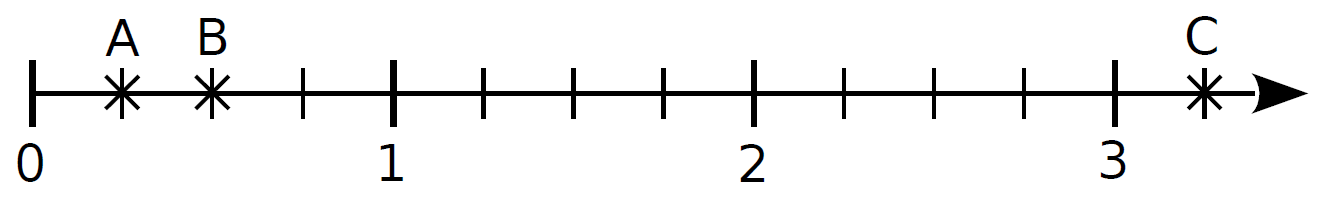
Sur la demi-droite ci-dessus, l'unité est partagée en $4$ parts égales. Pour trouver l'abscisse d'un point, on compte le nombre de parts depuis l'origine.
Le point $A$ a pour abscisse $\frac{1}{4}$.
Le point $B$ a pour abscisse $\frac{2}{4}$.
Le point $C$ a pour abscisse $\frac{13}{4}$.
2. La fraction-quotient
Les écritures fractionnaires sont liées à une opération : la division. Par exemple, la fraction $\frac{3}{2}$ possède une écriture décimale. Pour obtenir cette écriture décimale, on effectue une division : $\frac{3}{2}=3\div 2=1,5$.
Certaines fractions ne possèdent pas d'écriture décimale. Par exemple, $\frac{10}{3}=3,333...$ donc $\frac{10}{3}$ ne possède pas d'écriture décimale car la division de $10$ par $3$ ne se "termine pas".
Remarquons également que $\frac{3}{2}$ est le nombre qui multiplié par $2$ donne $3$. En effet, $\frac{3}{2}\times 2=3$. Plus généralement, on peut écrire la définition suivante.
Le quotient de $a$ par $b$ est le nombre qui multiplié par $b$ donne $a$. Ainsi, $\frac{a}{b}\times b=a$.
3. Écritures fractionnaires égales
a) Propriété fondamentale
On ne change pas un quotient quand on multiplie (ou divise) le numérateur et le dénominateur de son écriture fractionnaire par un même nombre non nul.
Traduit mathématiquement, si $a$, $b$ et $c$ sont des nombres tels que $b\ne 0$ et $c\ne 0$, alors $\frac{a}{b}=\frac{a\times c}{b\times c}$ et $\frac{a}{b}=\frac{a\div c}{b\div c}$.
b) Simplifier une fraction
Simplifier une fraction c'est transformer une première fraction en une seconde qui lui est égale et dont le numérateur et le dénominateur sont inférieurs à ceux de la première. Pour simplifier une fraction, on divise son numérateur et son dénominateur par un même nombre entier non nul.
Exemple
On veut simplifier autant que possible la fraction $\frac{18}{24}$. Expliquons-le de deux façons différentes.
Première façon : en divisant le numérateur et le dénominateur de cette fraction par un même nombre. On écrit $\frac{18}{24}=\frac{18\div 6}{24\div 6}=\frac{3}{4}$.
Seconde façon : en décomposant le numérateur et le dénominateur. On écrit $\frac{18}{24}=\frac{3\times 6}{4\times 6}=\frac{3}{4}$.
c) Diviser par un nombre décimal non entier
La propriété énoncée dans la partie a) permet d'effectuer des divisions où le diviseur est un nombre décimal non entier.
Exemple
On souhaite diviser $39,625$ par $12,5$. On peut écrire $39,625\div 12,5=\frac{39,625}{12,5}=\frac{39,625\times 10}{12,5\times 10}$ d'après la propriété.
Puis, $\frac{39,625\times 10}{12,5\times 10}=\frac{396,25}{125}=396,25 \div 125$ qui est une division que l'on sait poser et effectuer.
Ainsi, $39,625\div 12,5=396,25\div 125=3,17$.