Sommaire
Cliquez sur le titre d'une partie pour accéder directement à son contenu.
1. Vocabulaire, notations et représentations
a) Objets élémentaires de la géométrie
Lorsqu'on parle d'objets géométriques, on parle de points, de segments, de droites, de demi-droites, mais aussi de polygones, de cercles, etc. Les objets géométriques ne doivent pas être confondus avec les outils mathématiques qui sont la règle, l'équerre, le compas, le rapporteur, etc. Dans ce chapitre, nous n'étudierons que des objets élémentaires (simples).
Le point
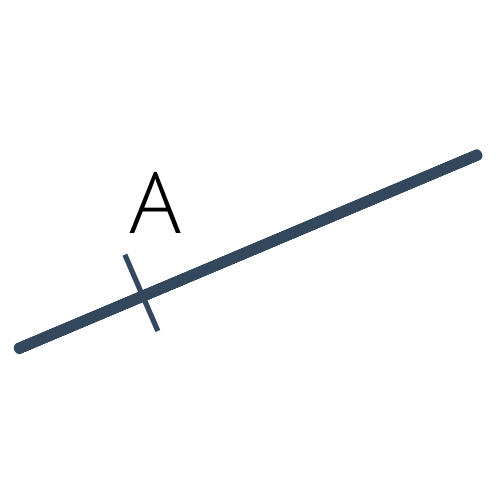
L'objet géométrique le plus simple est le point. Un point est généralement représenté par une croix ; son nom est écrit à côté de celui-ci, comme illustré ci-dessous. Un point se notera simplement à l'aide d'une lettre en majuscule. On écrit $A$ pour parler du point $A$.

Quand un point est placé sur un segment, une droite ou une demi-droite, il peut également être représenté de la façon illustrée ci-dessous.
Sur certains logiciels de géométrie, comme GéoGébra, les points sont représentés avec des ronds. On évitera cette représentation sur du papier car elle manque de précision pour les tracés.
La droite
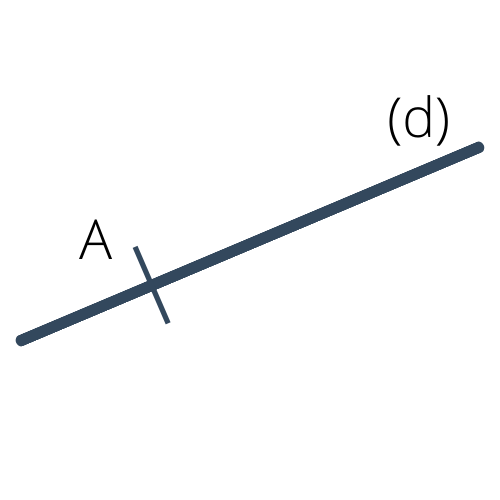
Une droite est un ensemble infini de points tous alignés. Elle se représente par une ligne qu'on prolonge au maximum pour signifier son caractère "infini", comme illustré ci-dessous. Une droite se notera à l'aide de parenthèses. On écrit $(d)$ pour parler de la droite $(d)$.
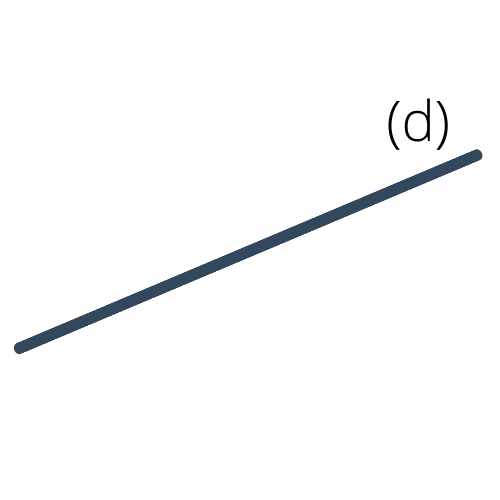
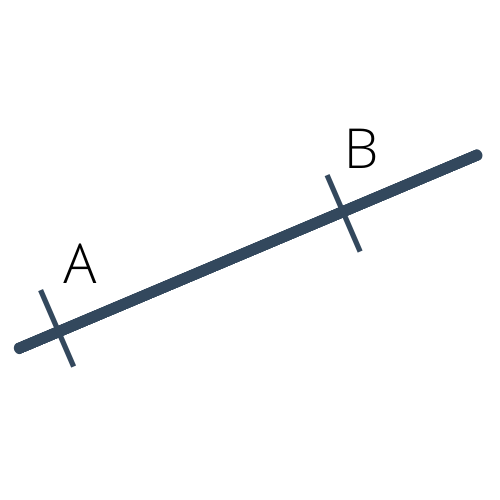
Deux points étant donnés, il existe une unique droite passant par ces deux points. Cette droite peut se noter $(AB)$ ou $(BA)$.
Le segment
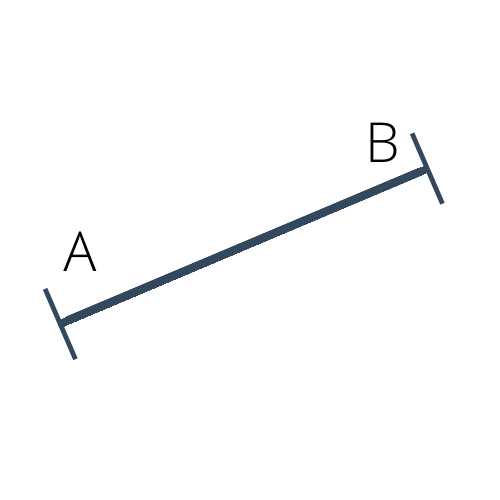
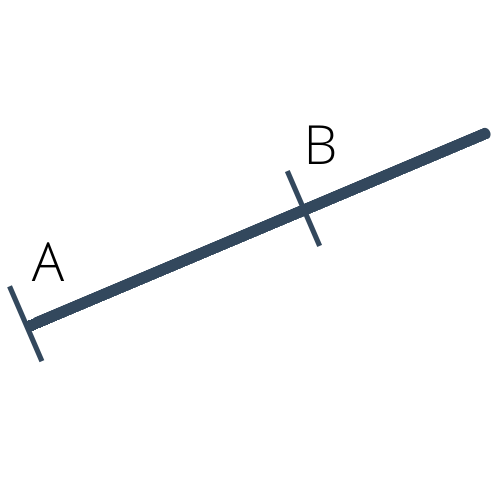
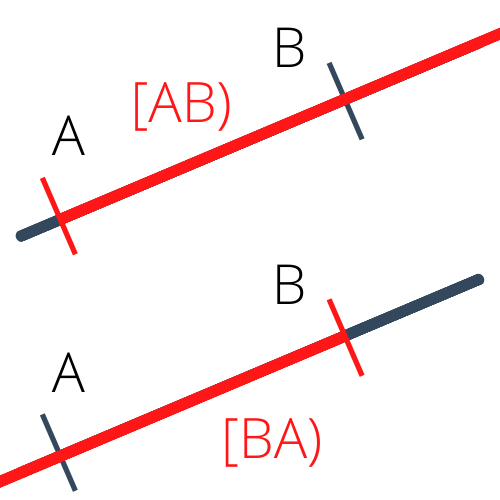
Un segment de droite est une portion de droite délimitée par deux points qu'on appelle extrémités de ce segment. Un segment qui relie deux points $A$ et $B$ est noté $[AB]$ ou $[BA]$. Il se dessine de la façon illustrée ci-dessous.
La demi-droite
Une demi-droite est une portion de droite limitée d'un seul côté par un point appelé origine. La demi-droite d'origine $F$ et passant par $G$ est notée $[FG)$ (on écrit l'origine du côté du crochet). Elle se dessine de la façon illustrée ci-dessous.
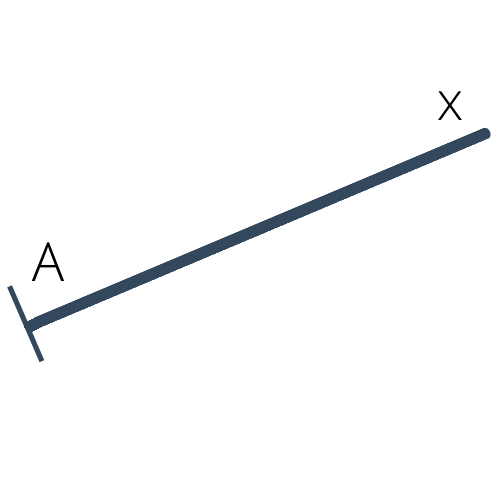
Parfois, on parler de la demi-droite d'origine $A$ et de direction $x$ et on note $[Ax)$. Cela se représente de la façon illustrée ci-dessous.
Contrairement à la droite, on ne peut pas inverser l'ordre des lettres dans la notation : écrire $[AB)$ ou $[BA)$ ne désigne PAS la même demi-droite !
Relation d'appartenance
Le symbole $\in$ signifie "appartient à" et le symbole $\notin$ signifie "n'appartient pas à". Il peut s'utiliser pour traduire l'appartenance ou non d'un point à un autre objet géométrique.
Sur ce premier dessin, le point $A$ appartient à la droite $(d)$. On note $A\in(d)$.
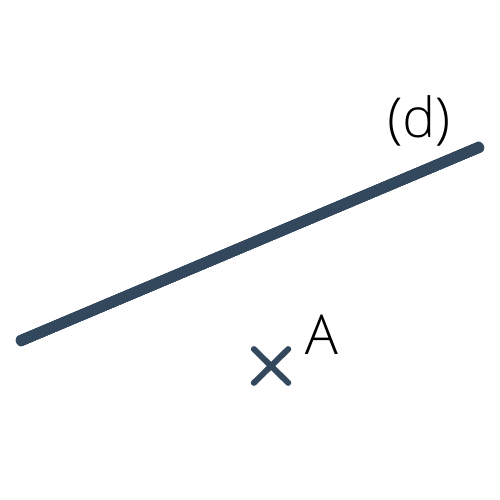
Sur ce second dessin, le point $A$ n'appartient pas à la droite $(d)$. On note $A\notin(d)$.
b) Points alignés
Trois points (ou plus) sont dits alignés s’ils appartiennent à une même droite.
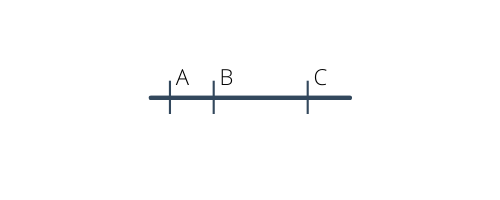
Sur ce premier dessin, les points $A$, $B$ et $C$ sont alignés car ils appartiennent à la même droite.
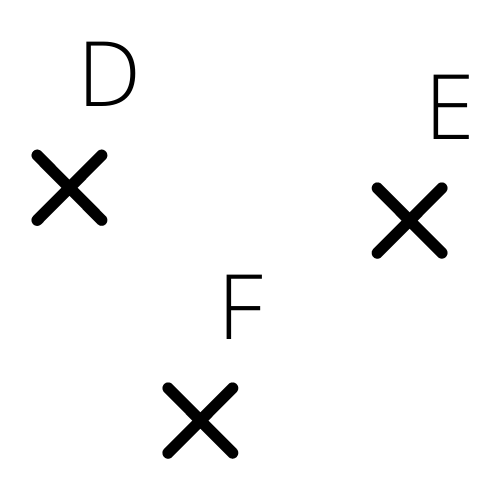
Sur ce second dessin, les points $D$, $E$ et $F$ ne sont PAS alignés.
2. Droites sécantes, droites perpendiculaires et droites parallèles
Étudier la position relative de deux droites, c'est étudier la position de l'une par rapport à l'autre.
Droites sécantes
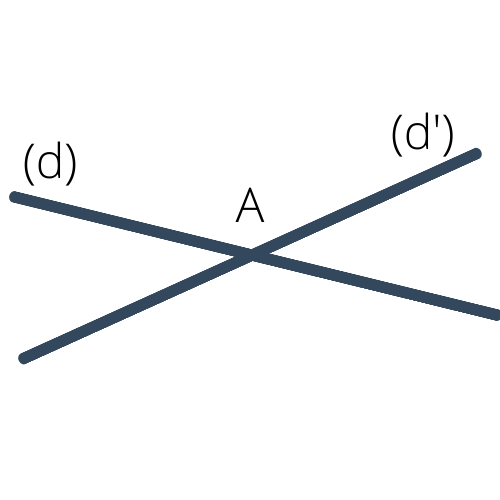
Deux droites sont dites sécantes lorsqu'elles n'ont qu'un seul point en commun. Ce point est appelé leur point d'intersection. Sur le dessin ci-dessous, les droites $(d)$ et $(d')$ sont sécantes. Leur point d'intersection est le point $A$.
Droites perpendiculaires
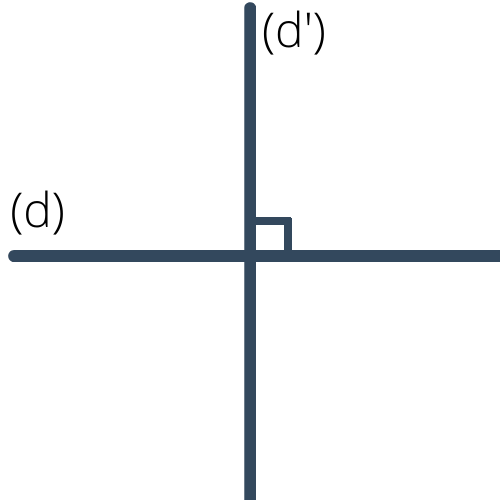
Deux droites sont dites perpendiculaires si elles se coupent en formant quatre angles droits. Des droites perpendiculaires sont des droites sécantes particulières. Sur le dessin ci-dessous, les droites $(d)$ et $(d')$ sont perpendiculaires. On peut noter $(d)\perp(d')$.
Droites parallèles
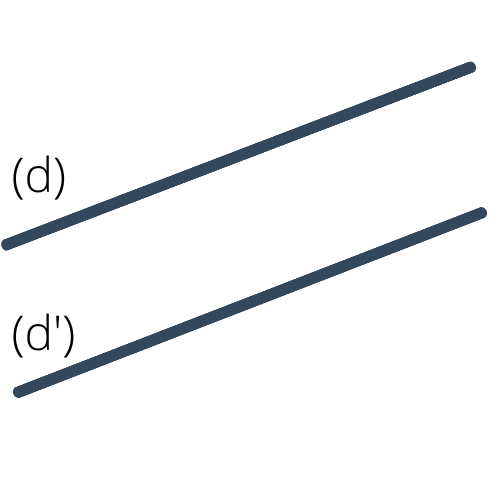
Deux droites sont dites parallèles si elles ne sont pas sécantes. Deux droites parallèles ne se "rencontrent jamais". Sur le dessin ci-dessous, les droites $(d)$ et $(d')$ sont parallèles. On peut noter $(d)\parallel(d')$.
3. Construire deux droites perpendiculaires
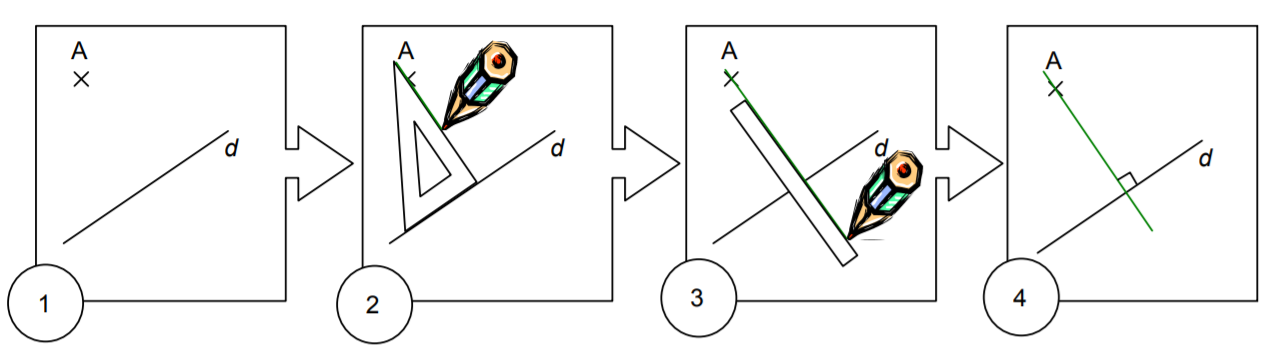
Les étapes suivantes expliquent comment construire la droite perpendiculaire à $(d)$ passant par le point $A$. Il faut utiliser deux outils : la règle et l'équerre.
4. Construire deux droites parallèles
Les étapes suivantes expliquent comment construire la droite parallèle à $(d)$ passant par le point $A$. Il faut utiliser deux outils : la règle et l'équerre.

5. Propriétés
Si deux droites sont parallèles, toute droite qui est perpendiculaire à l’une est alors perpendiculaire à l’autre.
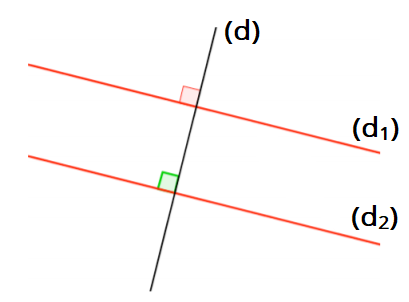
On sait que : $\left(d_1\right)\parallel\left(d_2\right)$ et $\left(d\right)\bot\left(d_1\right)$ (tracé en rouge).
On conclut que : $\left(d\right)\bot\left(d_2\right)$ (codage en vert).
Si deux droites sont perpendiculaires à une même droite, alors ces deux droites sont parallèles entre elles.
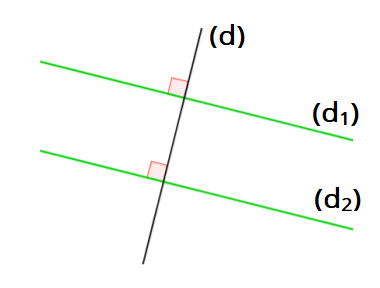
On sait que : $\left(d_1\right)\bot\left(d\right)$ et $\left(d_2\right)\bot\left(d\right)$ (codage en rouge).
On conclut que : $\left(d_1\right)\parallel\left(d_2\right)$ (tracé en vert).
Si deux droites sont parallèles à une même droite, alors ces deux droites sont parallèles entre elles.
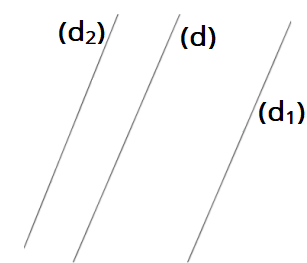
On sait que : $\left(d_1\right)\parallel\left(d\right)$ et $\left(d_2\right)\parallel\left(d\right)$.
On conclut que : $\left(d_1\right)\parallel\left(d_2\right)$.