Sommaire
Cliquez sur le titre d'une partie pour accéder directement à son contenu.
1. Rappels sur les nombres entiers
a) Le système décimal et la numération de position
Le système décimal utilise dix chiffres : 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 et 9. Ces dix chiffres permettent d’écrire tous les nombres que l’on connaît en classe de 6ème !
$327,65$ est un nombre qui s’écrit avec 5 chiffres différents.
La position d’un chiffre dans un nombre est appelée son rang et a une signification importante. Le tableau suivant est à connaître par cœur.

Dans l’exemple du tableau :
- Le chiffre des centaines est $7$.
- Le chiffre des dizaines de millions est $4$.
- Le nombre de centaines est $496 587$ (attention : ne pas confondre avec le chiffre des centaines qui est $7$).
Sur le même exemple, on peut effectuer une décomposition :
49 658 723 = 4 × 10 000 000 + 9 × 1 000 000 + 6 × 100 000 + 5 × 10 000 + 8 × 1 000 + 7 × 100 + 2 × 10 + 3
b) Les grands nombres
Pour lire plus facilement les grands nombres, on regroupe les chiffres « par 3 » en partant de la droite.
On préférera écrire 49 658 723 plutôt que 49658723…
Il existe une infinité de nombres ! Nous ne pouvons pas tous les citer... mais voici quelques grands nombres :
$1$ billion (1 000 000 000 000)
$1$ billiard ($1$ suivi de $15$ zéros)
$1$ googol ($1$ suivi de $100$ zéros)
2. Fractions décimales
Une fraction décimale est une fraction dont le dénominateur est 1 ; 10 ; 100 ; 1 000 ; 10 000 ; etc.
a) Les dixièmes
Quand on coupe une unité en $10$ parts égales, on obtient des dixièmes. Un dixième peut se noter $\frac{1}{10}$ ou $0,1$.
Sachant que dans une unité, il y a $10$ dixièmes, on peut écrire $10\times\frac{1}{10}=\frac{10}{10}=1$.
De la même façon, on peut écrire $10\times0,1=1$.

b) Les centièmes
Quand on coupe une unité en $100$ parts égales, on obtient des centièmes. Un centième peut se noter $\frac{1}{100}$ ou $0,01$.
Sachant que dans une unité, il y a $100$ centièmes, on peut écrire $100\times\frac{1}{100}=\frac{100}{100}=1$.
De la même façon, on peut écrire $100\times0,01=1$.

b) Les millièmes
Quand on coupe une unité en 1 000 parts égales, on obtient des millièmes. Un millième peut se noter $\frac{1}{1000}$ ou $0,001$.
Sachant que dans une unité, il y a 1 000 millièmes, on peut écrire $1000\times\frac{1}{1000}=\frac{1000}{1000}=1$.
De la même façon, on peut écrire $1000\times0,001=1$.
3. Nombres décimaux
a) Vocabulaire et tableau de numération
Un nombre qui peut s’écrire sous la forme d’une fraction décimale est appelé un nombre décimal. Un nombre décimal possède aussi une écriture décimale dans laquelle la virgule permet de repérer le chiffre des unités. Le tableau ci-dessous « prolonge » le tableau pour les nombres entiers.
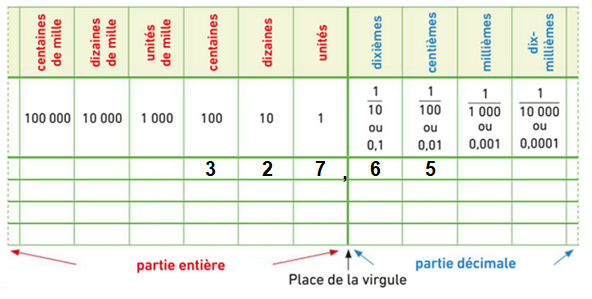
$327,65$ est un nombre décimal car il peut s’écrire $\frac{32765}{100}$.
- Sa partie entière est $327$. Sa partie décimale est $0,65$.
- Son chiffre des dizaines est $2$ et son chiffre des dixièmes est $6$, etc.
- Son nombre de dizaines est $32$.
Un nombre entier est un nombre dont la partie décimale est nulle (c’est-à-dire qu’elle vaut $0$).
b) Zéros facultatifs (parfois appelés zéros inutiles)
On ne change pas la valeur d’un nombre si l’on supprime ou si l’on ajoute des zéros à gauche de sa partie entière ou à droite de sa partie décimale.
$015,89 = 15,89$ (on a supprimé un zéro à gauche de la partie entière)
$13,1000 = 13,1$ (on a supprimé des zéros à droite de la partie décimale)
$14,0 = 14$ (on a supprimé un zéro à droite de la partie décimale et donc la virgule)
Un nombre entier est un nombre décimal particulier ! Par exemple le nombre entier $5$ est un nombre décimal car il peut s’écrire $\frac{15}{1}$ ou $15,0$.
c) Les différentes écritures d'un nombre décimal
Les explications données dans les parties précédentes permettent de donner de nombreuses écritures d’un même nombre décimal.
On peut écrire $259,38$ de différentes façons.
Son écriture décimale est $259,38$.
On peut le décomposer : 259,38 = 2 × 100 + 5 × 10 + 9 + 3 × 0,1 + 8 × 0,01.
On peut l’écrire sous forme de fraction décimale : $\frac{25938}{100}$ ou $\frac{259380}{1000}$.
On peut l’écrire comme la somme de sa partie entière et de sa partie décimale : $259,38 = 259 + 0,38$.
On peut l’écrire comme la somme d’un entier et d’une fraction décimale inférieure à $1$ :
$259,38 = 259 + \frac{38}{100}$ (on peut aussi décomposer $259,38 = 259 + \frac{3}{10} + \frac{8}{100}$).
Pour passer d’une écriture à une autre, on utilisera un tableau de numération si besoin.